Supernumerary Rainbows

beautiful picture of the side of a rich rainbow arc with thinner fainter rainbows on its inside edge. the sun is casting golden light on the trees behind the roof of a house. John Entwistle

Supernumerary rainbows are the faint rainbows that can sometimes be seen under the primary rainbow. They occur when the water droplets are smaller than 1mm wide. Supernumeraries & Drop Size - AtOpt

At the bottom of my primary rainbows page I illustrate how each color makes a slightly different sized cone of concentrated light (which we see head on as a circle) and how they overlap to form a rainbow. Primary rainbows with supernumeraries overlap very similarly, each color is simply in banded rings (which are nested cones).

seven rings with two rings nested in each. The largest is the red rings, and the smallest is the violet rings.
The rings overlapped so that they form a rainbow with two smaller fainter rainbows nested inside of it. animation of the rings superimposing over each other, starting with violet, resulting in a rainbow with smaller fainter rainbows nested inside of it.

This illustration shows the colors nesting perfectly with each other, however, in reality, they do overlap some, washing the colors of the supernumerary rainbows out, as shown in the next diagrams.

diagram showing how the colors of light in a rainbow overlap for large water drops and small ones. Primary Colors (1), Supernumerary Colors (2) - AtOpt

These two simulations show the concentration of each color and how they overlap to form a primary rainbow made from large verus small drops. The left is a primary rainbow formed by larger water droplets, and the right is a primary rainbow with supernumary bands formed from 0.7 mm droplets. Both feature staggered colors, allowing a rainbow to form instead of just overlapping fully to make white light, but in the supernumary simulation, each wavelength of light is banded. Notably, further from the primary, the supernumerary bands are more overlapped, creating washed out rainbows further out as the wavelengths mix more.

two diagrams showing the bands of light for two different drop sizes. One is for monochromatic blue, and the other is for a full rainbow. For both the rainbow and the blue, the 0.8mm drops create thinner bands, the supernumerary ones being very faint. the 0.4mm drops create wider bands and more saturated supernumeraries. Primary Rainbow Drop Size - AtOpt

Here two diagrams show the difference drop size makes on the width and clairity of supernumerary bands. The first diagram shows only teal to illustrate how this affects every color, and the second diagram shows all the colors overlapping to form a rainbow. The smaller the droplets, the wider the supernumary bands are spaced and the brighter they are. Conversely, larger droplets form thinner fainter bands. It is also important to note that supernumerary bands are more noticable when the raindrops are uniform in size, if they are too varied, their different banding patterns will overlap and wash each other out. Supernumeraries & Drop Size - AtOpt

So why exactly do smaller water droplets form bands of light and large ones don't? Well, wavelengths of light are very small (400nm-700nm) so only drops that are small will create a strong enough interference pattern that we can see with our eyes.

Waves

Light travels in waves, and waves can interact with other waves in what is called interference. They can combine with each other to create larger waves, or cancel each other out to make smaller waves.

diagram of two waves each of constructive and destructive interference.

This diagram shows contructive and destructive interference. When the peaks and valleys of two waves line up, they add together, increasing the amplitude of the wave (left). When a peak lines up with another waves valley, they cancel each other out, decreasing the amplitude of the resultant wave (right).

Interference does not change wavelength, just the height of the peaks and valleys, which affects the brightness of the light. Tall waves are bright, whereas shallow waves are dim (a flat line is no light).

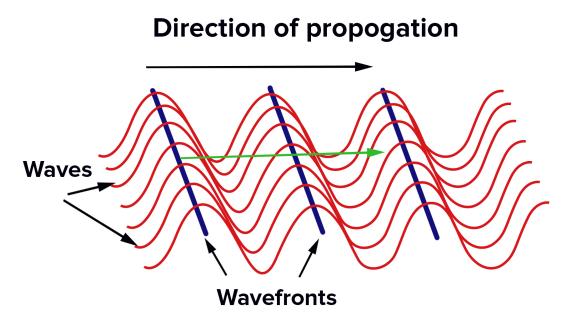
diagram showing waves traveling along side of each other so that their peaks and valleys line up

Consider this diagram again, showing how waves form wavefronts. The lines in the next diagram represent the peak of a wavefront.

straight wavefronts entering a waterdrop where they become curved and exit curved. The Mathematics of Rainbows - AMS

Most notable is the fact that when the wavefronts from the sun hit the curved surface of the drop, they too become curved. The smaller the drop, the more severe the curve of the surface is.

We know that once the exiting rays hit 42 deg from the entrance rays, the light folds back in on itself and flares back upward, making a hard line that forms the primary bow. This is where we get the overlap of wavefronts in this diagram.

diagram of many rays entering a water drop. They bend slighty inside the drop, and then some exit on the other side, bending a little more and flaring out from another. Before exiting the drop, some rays reflect off of the back of it, and exit on the entrance side. These rays flare down and out from another, until hitting a line where they start to flare upwards. Rainbow Caustics - AtOpt

Consider this diagram again (first mentioned in secondary and higher order rainbows). It shows how upon exit, the reflected rays hit a hard line and flare back up, overlapping the other reflected rays. This is a ray diagram, with just straight lines, unlike the previous it doesn't show light in its wave form. With illustrated wavefronts, we will see an interference pattern.

Wait a second, why do the wavefronts curve when entering a curved surface?

First lets go back to refraction, where when light hits a different material at an angle, said light bends. It doesn't bend when hitting the surface head on though.

Now lets consider the circular shape of a water drop and simplify it to a flat sided shape.

a circle next to a 20 sided polygon, which looks like a circle from far away.

Now like the ray diagram, light is going to enter the simplified drop at all positions (it also enters the "bottom" of the drop, but this mirrors the top and would make the diagram confusing with many overlapping lines).

the top left portion of the 20 sided polygon, with light coming at it horizonally from the left. It enters each side of the polygon, which forms sharper angles with the light, the closer to the top of the polygon the side is. The light is bent more within the shape when passing through the sharper angled sides

Here we see that the light bends more when entering a more angled surface, in order to keep the waves intact.

Of course a droplet is actually a circle (well, a sphere), so this change in bending angle occurs at every single point on the drop, forming curved wavefronts.

If we actually use math and formulas, we can calculate exactly how much one ray of light is bent when it enters at each angle, and again how much it is bent when it exits the drop, forming the straight line diagram above this sidenote. It will produce the same effect where eventually, once the light enters so close to the edge of the drop, it will exit the drop at such an angle that the exit path overlaps those of the previous ones.

wavefronts entering a water drop, reflecting off the back and exiting. They are straight before entering, and then curved according to the drop inside and exiting the drop. The curved lines overlap where they do in the previous diagram. Like a Bridge Over Colored Water: A Mathematical Review

Here the exit wavefronts are extended to show how they overlap. Where the curved lines overlap perfectly, showing the same amount of space between the lines as the non-overlapping waves, is constructive interference, the peaks and valleys of the wave add together to create stronger more intense light. Where the waves overlap so one line is directly in the midde of the space between two lines is destructive interference, a peak is directly overlapping the valley of the other wave and cancelling it out, making no light. The first place there is constructive interference is the caustic line, the primary rainbow. The second area of constructive interference is the first supernumerary band.

wavefronts entering two waterdrops of different sizes Like a Bridge Over Colored Water: A Mathematical Review

Compare a rainbow to a cloudbow. Cloudbow drops are signifigantly smaller, making much wider intererence bands. The opposite is also true, the larger the drop, the more narrow the interence bands.

The interference pattern for large drops has such tight and narrow bands for each color, that they are too fine to distinguish. Instead, we see a glow inside of the rainbow. Being so narrow, even a slight variation in drop size washes the supernumerary bands out since these patterns will overlap.

Suggested Next Page: Fogbows